Postulat-postulat
Postulat adalah pernyataan dasar yang tidak dibuktikan, tetapi diperlukan untuk menjadi dasar pembuktian. Istilah yang kita pakai dalam sistem deduktif adalah aksioma.
Ada 5 postulat dalam sistem geometri Euclid, yaitu:
Ruas garis lurus dapat dibentuk dari satu titik ke titik yang lain.
Ruas garis dapat diperpanjang sepanjang-panjangnya.
Lingkaran dapat dibentuk menggunakan ruas garis sebagai jari-jari, dan salah satu titik ujungnya sebagai pusat lingkaran.
Semua sudut siku-siku adalah kongruen (sama dan sebangun).
Jika sebuah garis melalui dua garis lain, dan jumlah sudut dalam kedua garis tersebut pada sisi yang sama adalah kurang dari dua kali sudut siku-siku, maka kedua garis tersebut akan bertemu jika diperpanjang.
Mari kita melihat detailnya satu per satu.
Postulat 1: Ruas garis
Ruas garis lurus dapat dibentuk dari satu titik ke titik yang lain.
Postulat pertama ini sangat mudah dimengerti. Kalau kamu diperhadapkan pada dua titik yang berbeda seperti pada gambar di bawah ini:
Titik-titik ini bisa digeser lho!
Kamu dapat menghubungkannya menjadi sebuah ruas garis lurus.
Titik-titik ini bisa digeser lho!
Hal ini berlaku umum pada dua titik di manapun kedua titik tersebut berada. Cobalah tempatkan titik-titikmu sendiri pada media interaktif di atas.
Postulat 2: Perpanjangan garis
Ruas garis dapat diperpanjang sepanjang-panjangnya.
Ruas garis seperti pada postulat pertama memiliki dua ujung. Dalam contoh di bawah ini adalah titik A dan titik B.
Titik-titik ini bisa digeser lho!
Namun tidak ada yang membatasi bahwa garis yang kamu buat harus terbatas pada dua ujung tersebut. Kamu dapat memperpanjangnya ke satu maupun kedua arah sesuka hati.
Titik-titik ini bisa digeser lho!
Postulat 3: Lingkaran
Lingkaran dapat dibentuk menggunakan ruas garis sebagai jari-jari, dan salah satu titik ujungnya sebagai pusat lingkaran.
Ini artinya kalau kamu memiliki sebuah ruas garis GH seperti pada gambar berikut ini:

Kamu dapat menahan G pada tempatnya, kemudian membuat H berputar sesuka hatimu.
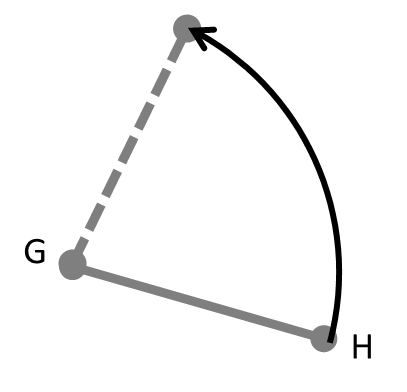
Jika kamu meneruskan putarannya, akan muncul bentuk lingkaran.

Kamu bisa mencobanya sendiri melalui media interaktif di bawah ini.
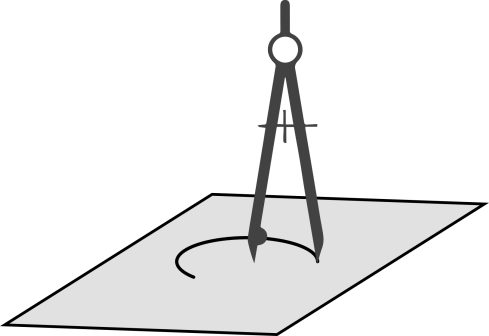
Ini adalah prinsip yang digunakan dalam jangka, yaitu menahan satu kaki jangka, sementara memutar kaki jangka yang lain.
Postulat 4: Sudut siku-siku
Semua sudut siku-siku adalah kongruen (sama dan sebangun).
Dua bentuk adalah kongruen kalau kamu bisa menumpuk kedua bentuk tersebut dan keduanya pas.
Di bawah ini ada dua sudut, yang disebut α dan β, keduanya siku-siku.
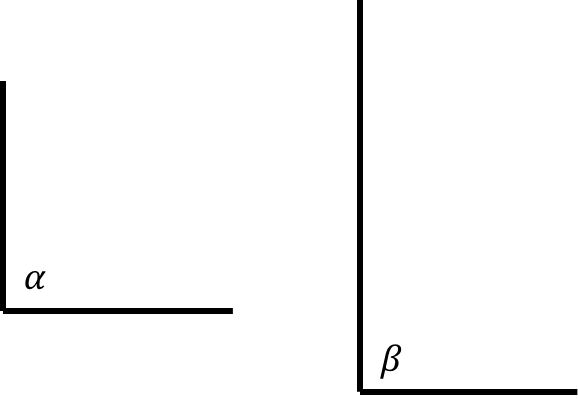
Kamu bisa memindahkan sudut α dan menumpuknya pada sudut β.
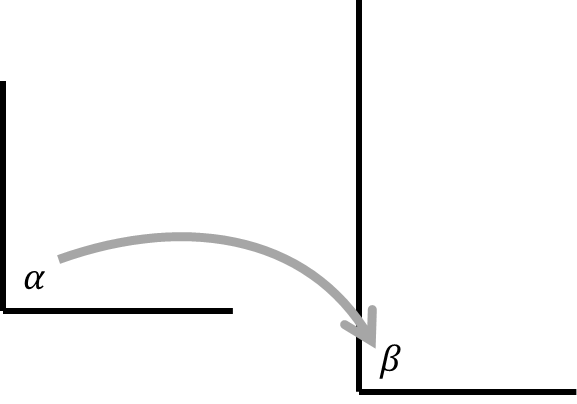
Kamu akan menemukan bahwa keduanya pas.
Postulat keempat ini memaksudkan bahwa segala macam sudut siku-siku yang dapat dibuat, apapun bentuknya, bagaimanapun posisinya, akan pas satu sama lain ketika kamu menumpuknya menjadi satu.
Postulat 5?
Postulat 5 lebih rumit dari postulat-postulat sebelumnya, sehingga kita akan bahas tersendiri dalam halaman berikutnya.
Berikutnya: Postulat 5: Garis sejajar